iOS: Introducing Stack Views Programmatically

As your iOS development skill is growing, I believe you use UIScrollView, UICollectionView, UITableView, and other native views regularly and proficiently in your applications. Yet, some iOS developers still don’t know what exactly UIStackView is, what it uses for or in which situation should we use UIStackView.
In this tutorial, I will introduce you to UIStackView - A view helps us to simplify our iOS layouts.
Let’s imagine you’re going to build an application that allows the user to add or remove views in run time. Remember how we will accomplish this task? We first have to remove all constraints in the relative area and update them all over again. Or remember the case where you implement the sign-in / sign-up view, you add many text fields and manually set constraints between those views. In such situations, UIStackView appears to be more useful than other views.
To demonstrate how to apply UIStackView to your projects, we’re going to build a simple application that allows the user to control smart devices in their home; Users can add or remove which room they want it to show in their list of control. The main key here is all actions of the user are executed in runtime dynamically. Additionally, instead of using Storyboard in this project, I’m going to use code dynamically along with the help of the AutoLayout framework (SnapKit - it is just a matter of preference). Let’s put aside other complex implementation, the application contains only two views: A login view and a home page. Also, there will be no logic code at all.
Key properties
To understand how a Stack View work, we first need to have a look at its properties. No matter what kind of the Stack View is (Horizontal or Vertical), there are four main properties: Axis, Spacing, Alignment, and Distribution. The following image summarizes the relative among those attributes.
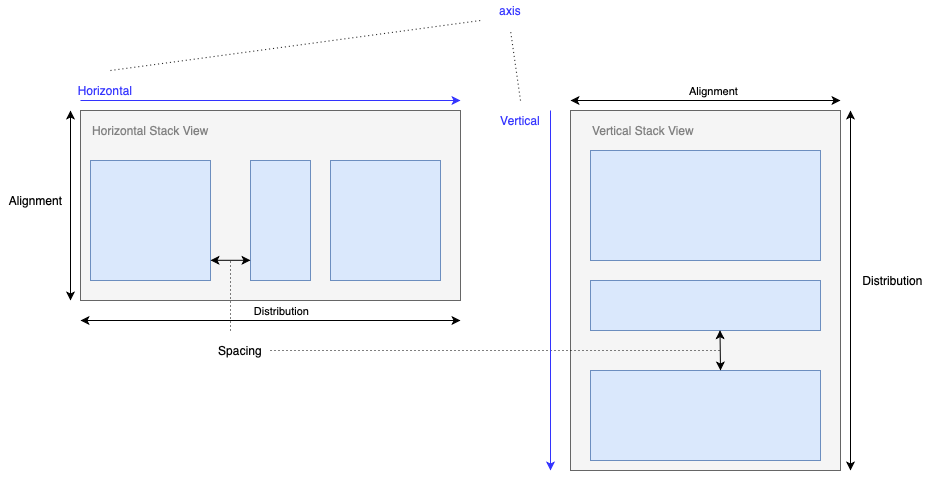
- Axis: determines the stack’s orientation, including Horizontal and Vertical.
- Spacing: determines the minimum space between the stack’s views.
- Alignment: determines the layout of the stack’s views perpendicular to its axis.
Both horizontal and vertical stack views have theFillandCenteroptions.- Fill: Stack’s arranged views will be resized so that they fit the stack view perpendicularly to its axis. The leading and trailing edges of vertically stacked items or the top and bottom edges of horizontally, respectively.
- Center: As the name suggests, center the stack’s views horizontally (Vertical stack) or vertically (Horizontal stack).
| Fill | Center |
|---|---|
 |
 |
There are some alignment options applied only for horizontal stack views:
- Top: As the name suggests, center the stack’s views horizontally (Vertical stack) or vertically (Horizontal stack).
- Bottom: As the name suggests, center the stack’s views horizontally (Vertical stack) or vertically (Horizontal stack).
- First baseline: A layout where the stack view aligns its arranged views based on their first baseline.
- Last baseline: A layout where the stack view aligns its arranged views based on their last baseline.
| Top | Bottom | First baseline | Last baseline |
|---|---|---|---|
 |
 |
 |
 |
 |
 |
Similarly, there are some alignment options worked for vertical stack views only:
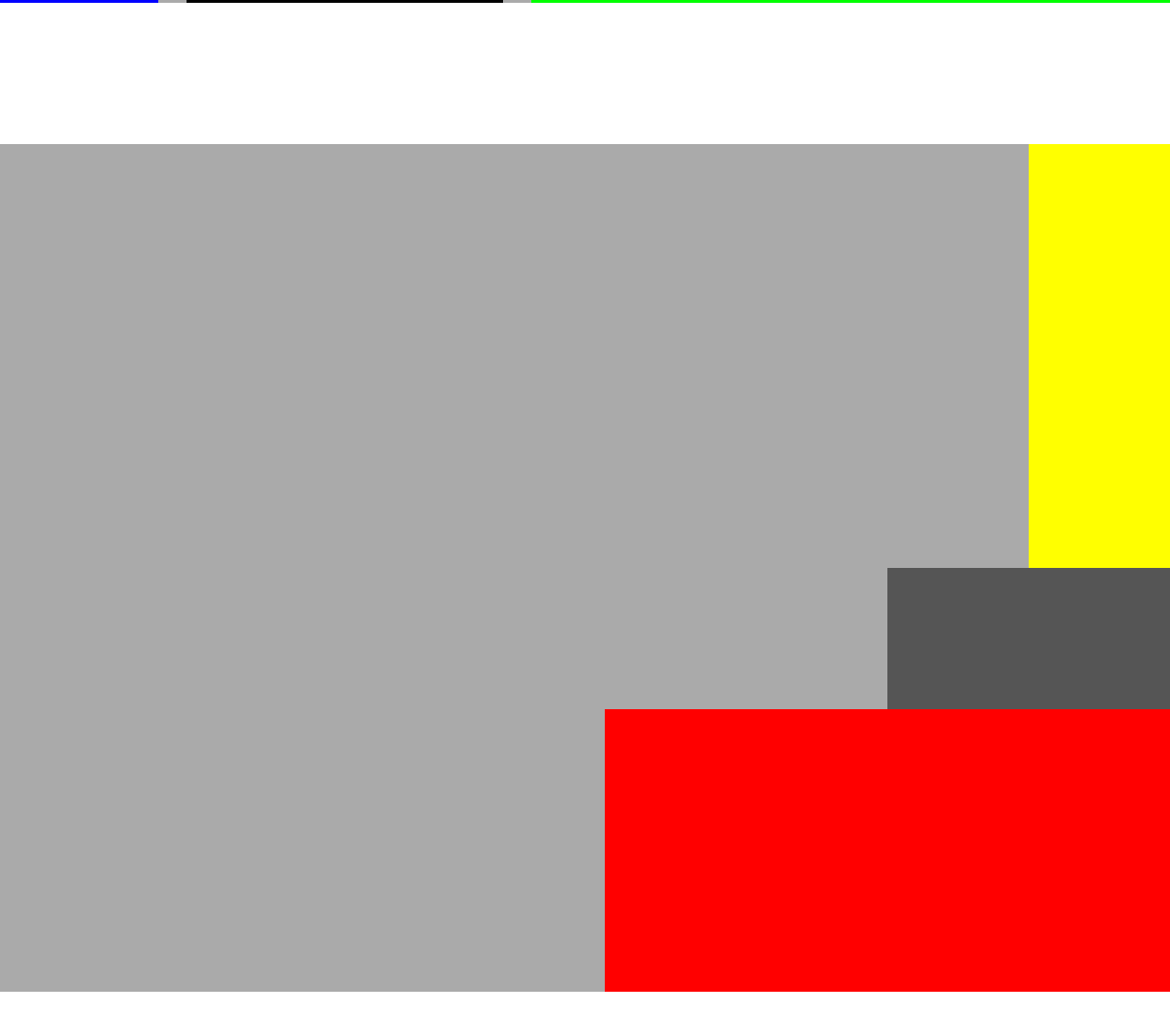
Leading: The stack view aligns the leading edge (Left) of its arranged views along its leading edge. Similar to top alignment for horizontal stacks.
Trailing: The stack view aligns the trailing edge (Right) of its arranged views along its leading edge. Similar to bottom alignment for horizontal stacks.
Leading Trailing 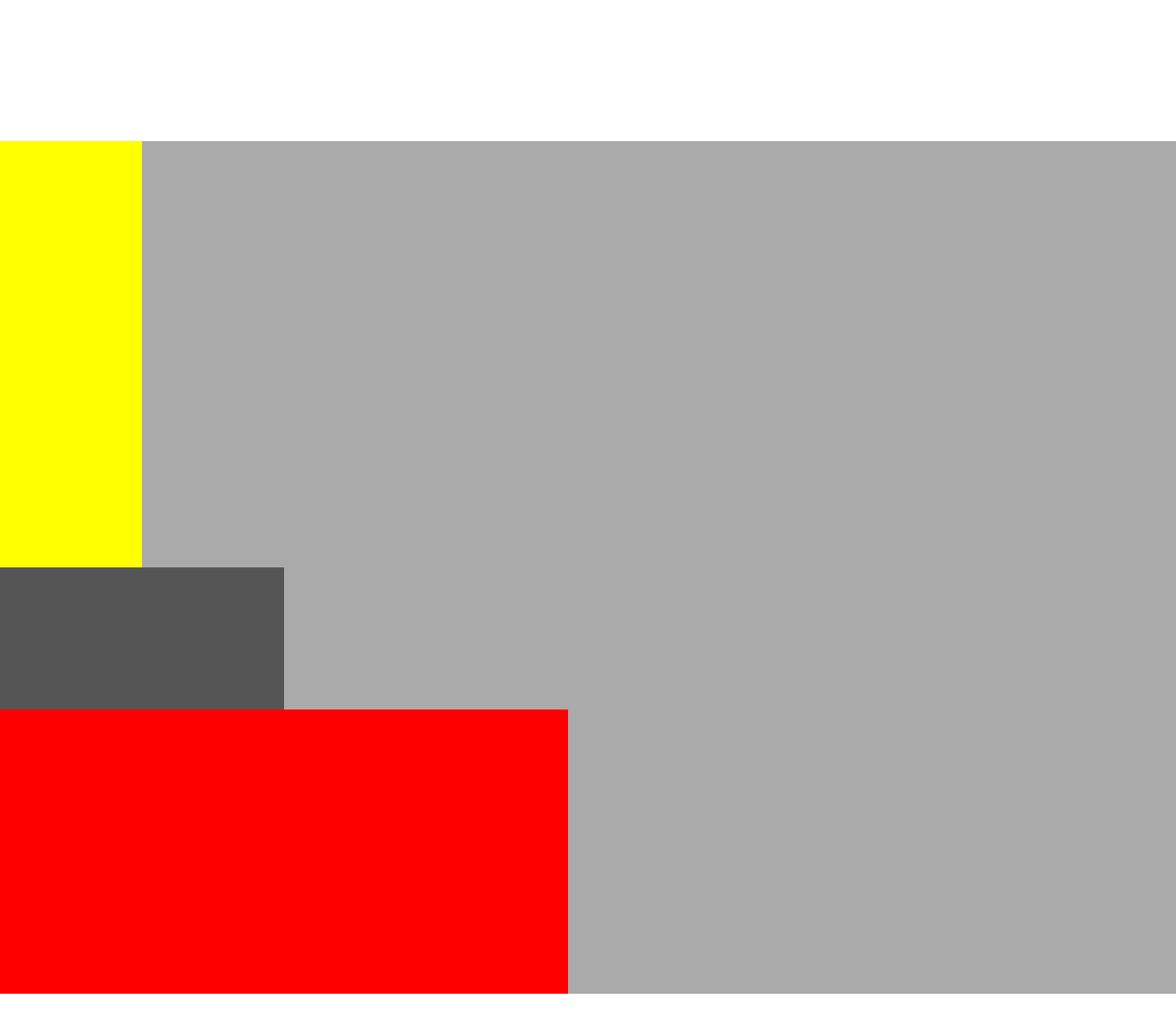
Distribution: determines the layout of the stack’s views along its axis. The subviews are all resized based on this setting.
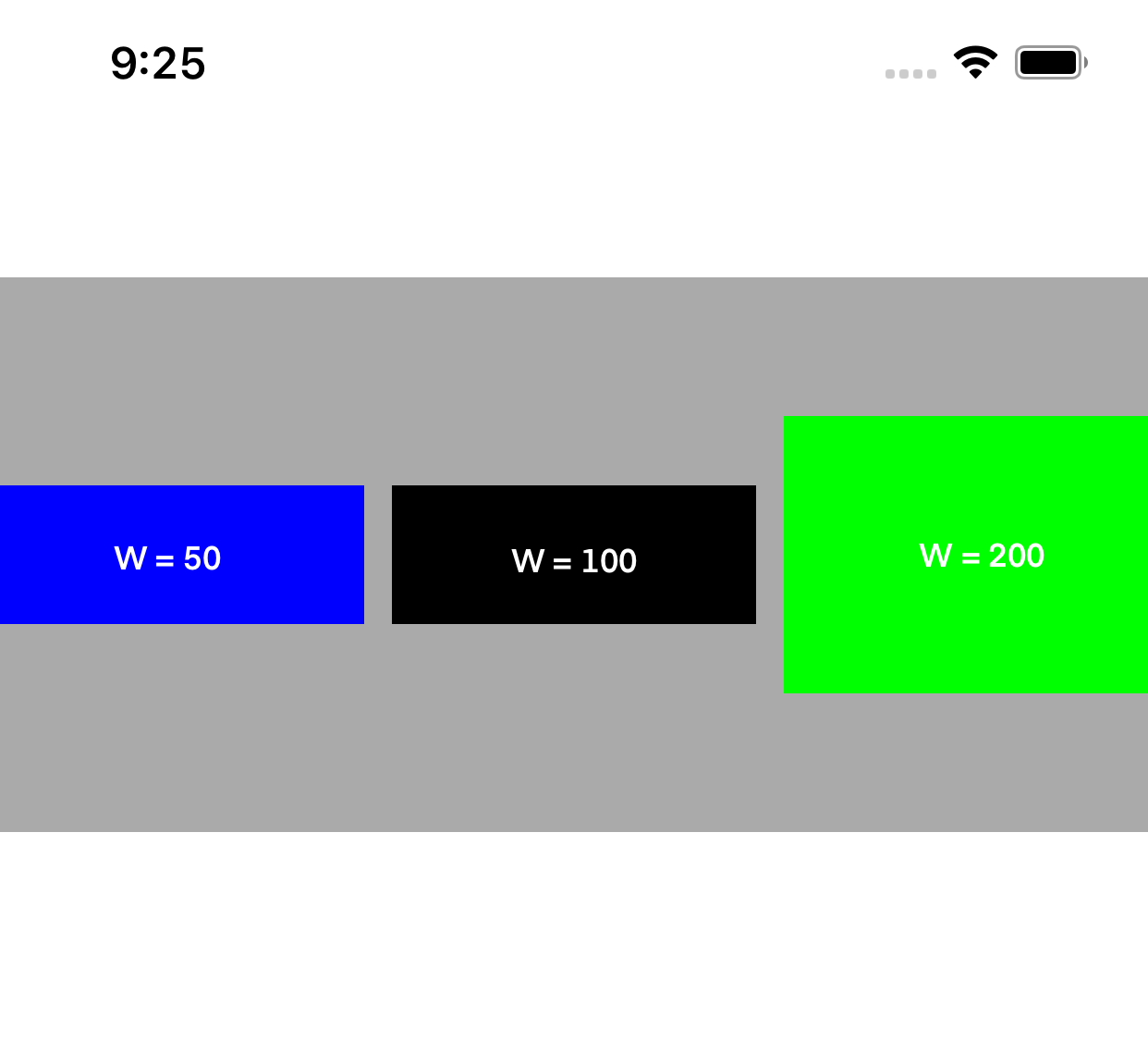
- Fill: This is set as the default distribution when a Stack View is created. When we put views inside a UIStackView with Fill set as the distribution, it will keep trying to stretch the size one of the views to fill the space.
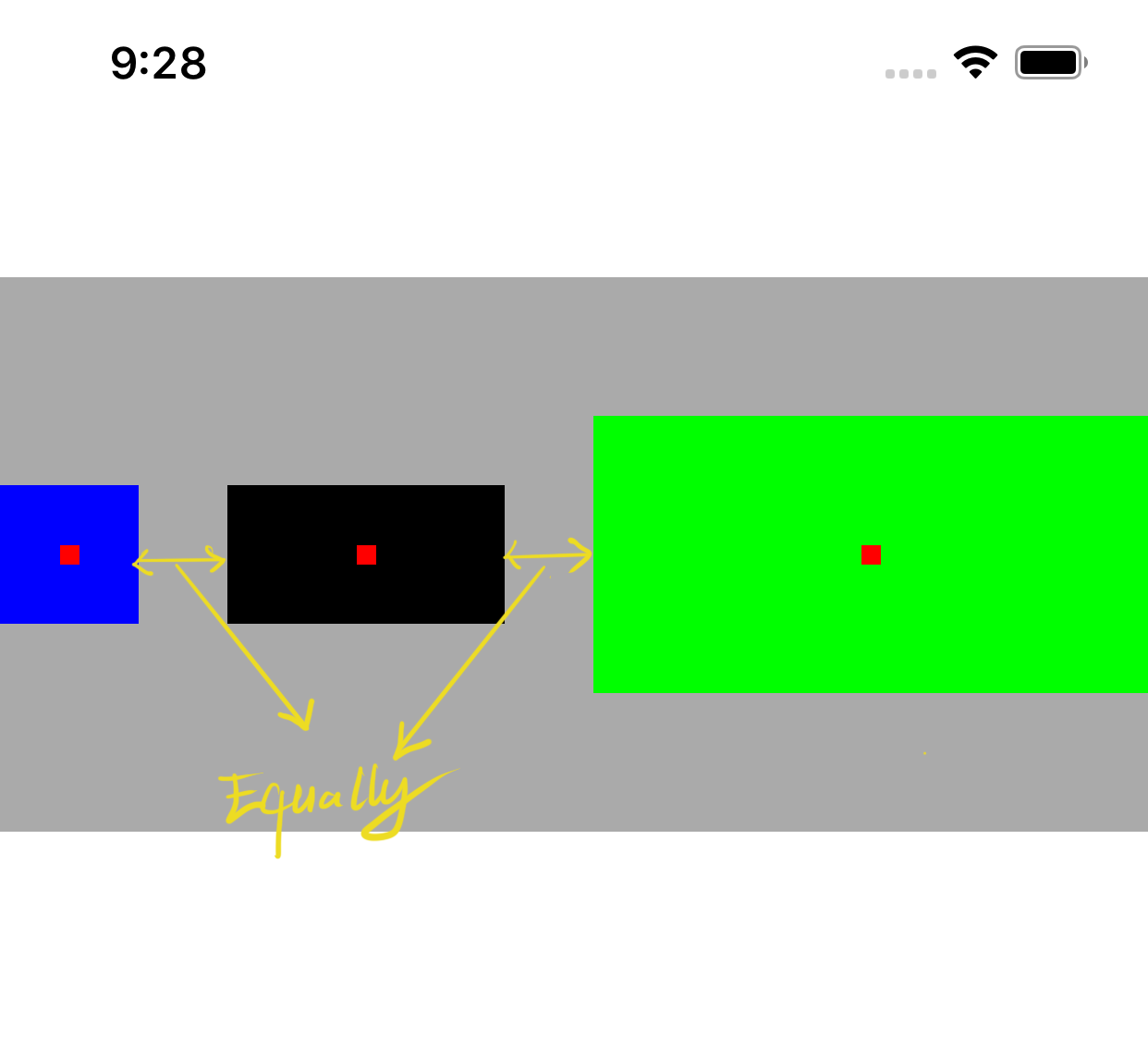
So the question is, what criteria will it base on to choose the view to resize? Content Hugging Priority (CHP) will be. To determine which view will be stretched, the stack view will rely on CHP for evaluation, the lower its priority, the more likely it is to be chosen. If all the views have the same CHP, the first one will be picked. - Fill Equally: Each control in a UIStackView will be of equal size.
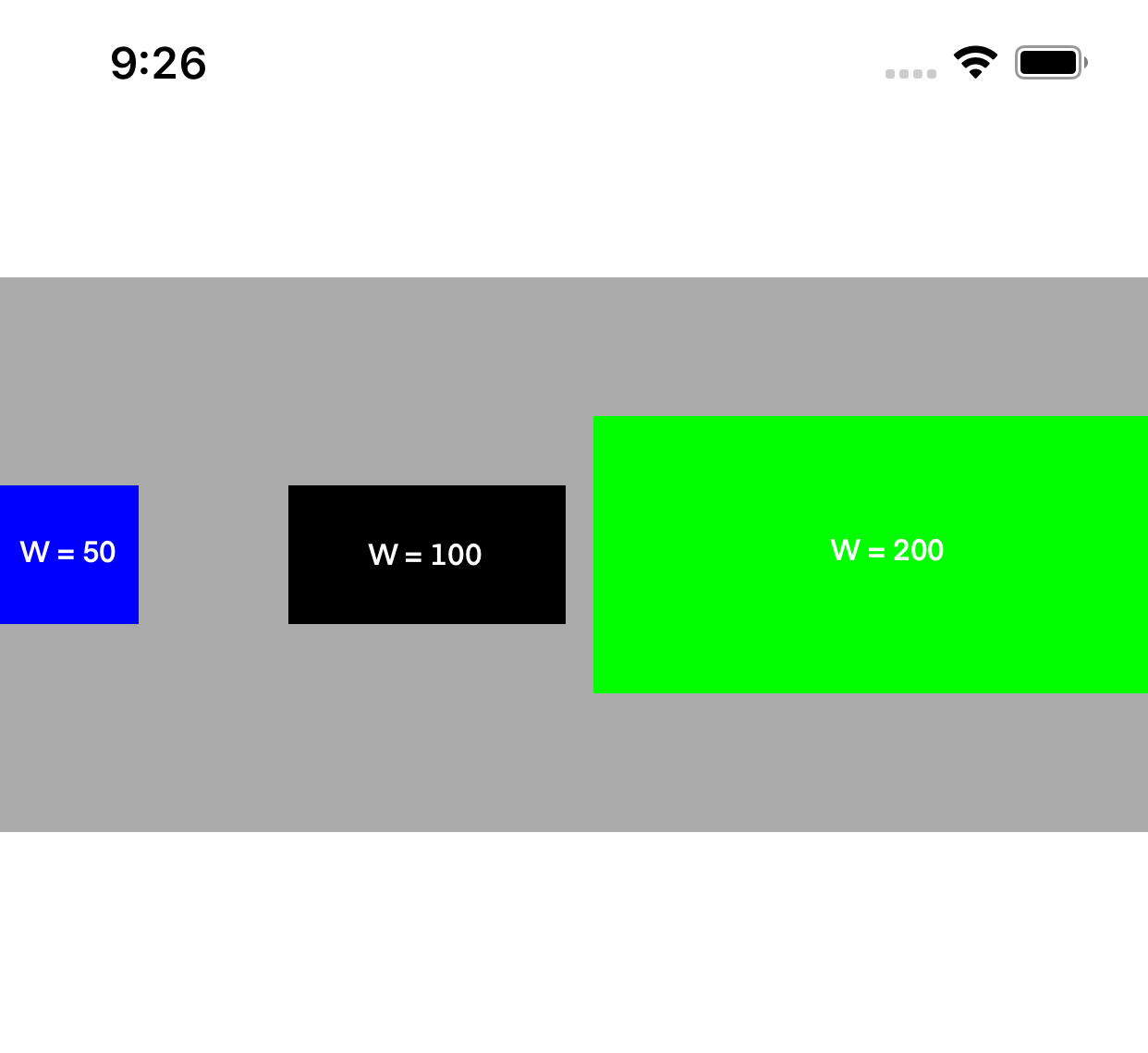
- Fill Proportionally: All the controls need to have an intrinsic content size, Stack view will ensure the controls maintain the same proportion.
- Equal Spacing: This distribution type will maintain equal spacing between the subviews.
- Equal Centering: This distribution type will maintain an equal space between the center of the subviews.
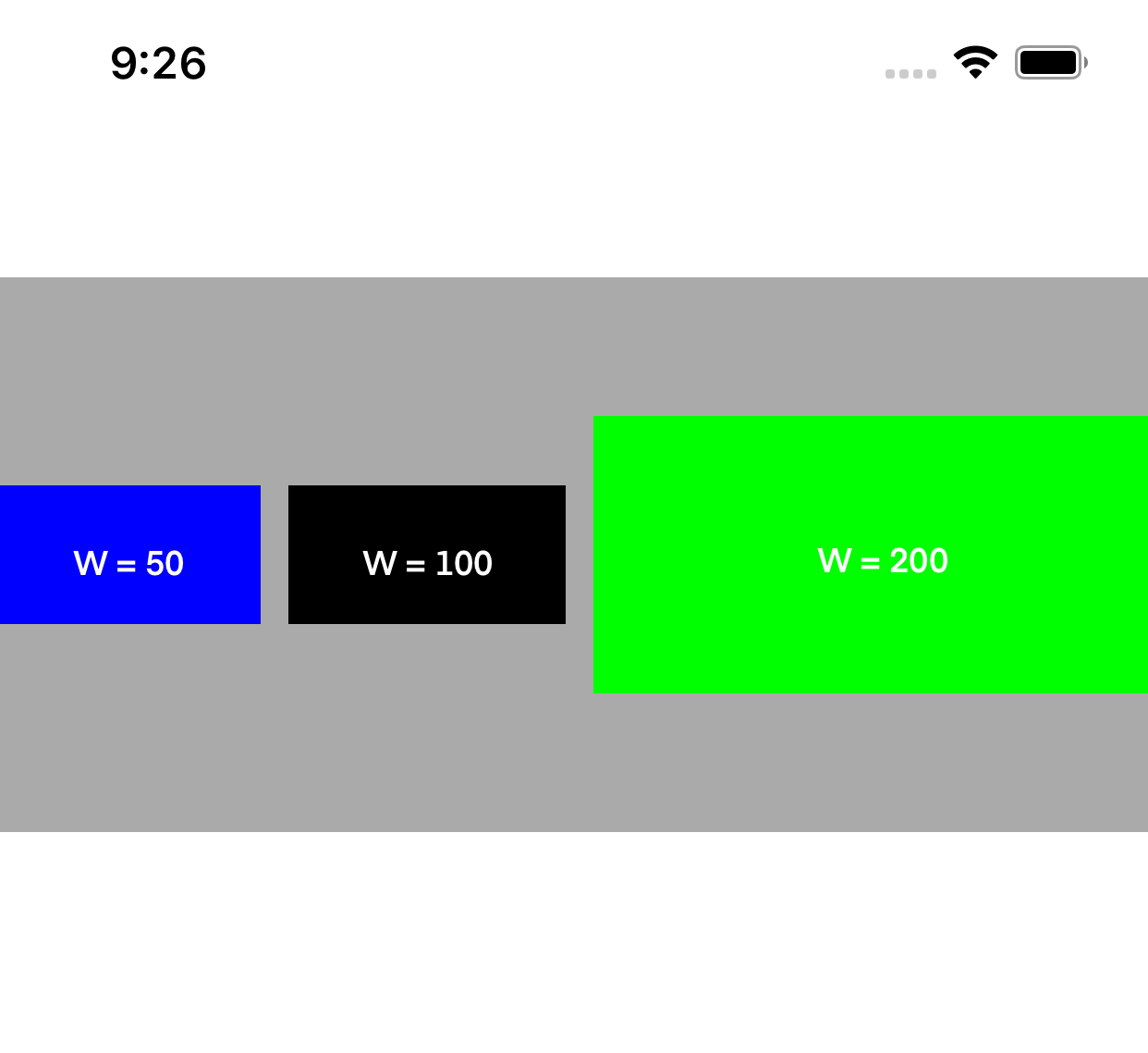
- Fill: This is set as the default distribution when a Stack View is created. When we put views inside a UIStackView with Fill set as the distribution, it will keep trying to stretch the size one of the views to fill the space.
| Fill | Fill Equally | Fill Proportionally |
|---|---|---|
 |
 |
 |
| Equal Spacing | Equal Centering |
|---|---|
 |
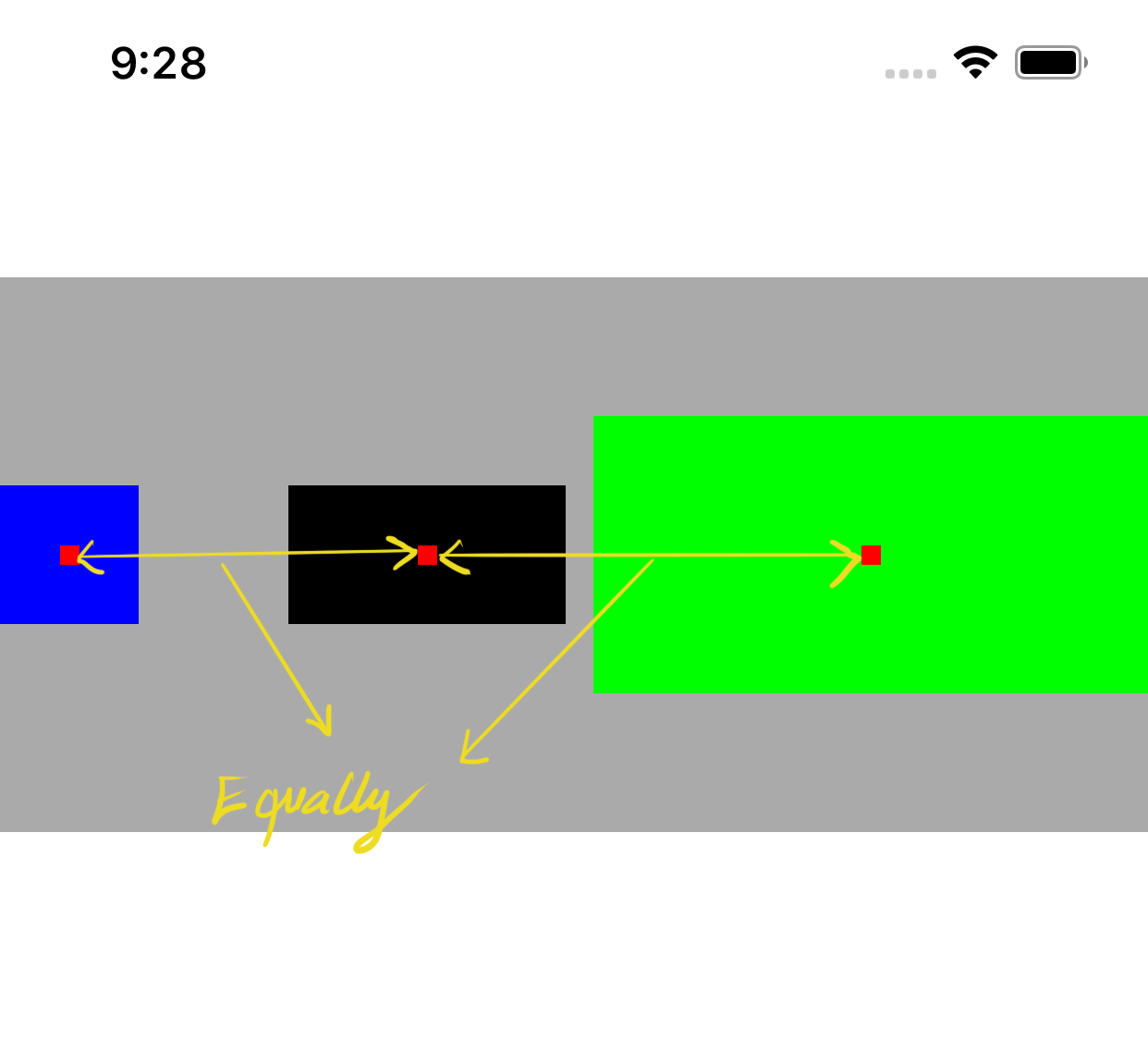 |
Note:
UIStackViewis a non-rendering view, which means you can not set the background-color property, or override thedrawmethod, etc.
Take to practice
Now, with that knowledge in mind, we’re going to apply it to an existed project that currently does not use UIStackView to arrange its view at all. By applying UIStackView into practice, we will really get an understanding of how a UIStackView works and what problems it can resolve.
Auto arrange views
The first thing UIStackView brings to us is the freedom from setting constraints for all views.
The login view is quite simple, it contains two text fields, a login button and some text labels.
Without using UIStackView, we have to manually set constraints for all those text fields.
1 | view.addSubview(lblLogin) |
But it’s still not a nightmare. Imagine now you want to add some other views, such as a label and a switch view to allow the user to remember the login session. We now have to alter all other views to insert those new views to the right place on the screen!
The task will be easier and simpler if we use StackView. Now let see how we can do it.
First, let’s add a new property to the Log in view controller.
1 | lazy var stackView: UIStackView = { |
Notice at [1], this is how we add arraged views to a stack view. Then, we just need to set contraints for the stackView.
1 | override func viewDidLoad() { |
In the future, if we want to add new views, we just need to put it to the arranged views array. As below.
1 | lazy var keepLoginStackView: UIStackView = { |
1 | // ... |
Can you see the differences? The codebase now is cleaner and more maintainable than the old one, isn’t it?
Dynamic views
Now switch to the case where we will implement the Home page of the application.
When the user presses the right button of the screen, a new view, which represents for a room to be controlled in this case, will be placed on the main page. The user can also remove any rooms in the list by pressing the “Remove” button. Inside each room, there is a “Hide” / “Show” button that allows hiding and showing the room image. Remember in the past where you have to implement a similar feature in your app without using UIStackView, what will you do? Somewhat painful! We first need to remove all constraints in the relative area and update them all over again.
Here is what we’re going to do with UIStackView, the main page contains a vertical stack view embedded inside a scroll view. Whenever the Add button is pressed, a new TaskView view will be added to this stack view.
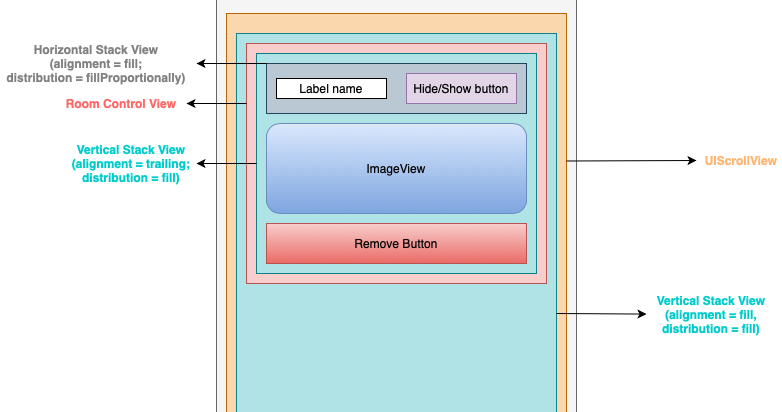
1 | func addMoreView() { |
We also need to set height constraints for this new view. Because the height of the view might be changed when the show/hide button is pressed, we need to define this constraint as lessThanOrEqualToConstant:value so that the stack view can adjust this height constraint.
1 | func onRemove(_ view: TaskView) { |
When the remove button on a task view is clicked, this view will be removed from the stack view. We can access all arranged views of a stack view by accessing arrangedSubviews property. We first loop for all arranged views and find the appropriate view which have the same address with the sender, then remove it from the super view. Additionally, I make a small animation, UIView.animate(withDuration:animations:), so that the transition looks more smooth and fancier than the last one.
By using the same approach, you can do the same thing when the user clicks on Show / Hide button to show/hide the image view. Let’s take a try by yourself.
Final though
In this tutorial, I introduced you to UIStackView - a subclass of UIView helping to manages the position and size of its arranged views. We also worked through a demonstration that takes UIStackView into practice. Now you get the idea of how the UIStackView works and what the UIStackView uses for, next times try to use UIStackView in your app to leverage its power. I will do, won’t you?
You can download the completed demo at Github,
Happy coding!